La división solo es una resta repetida

La matemática puede ser un tema intimidante para muchas personas. Hay tantas operaciones y conceptos que puede ser difícil saber por dónde empezar. Pero si entiendes los fundamentos, todo lo demás se vuelve más fácil. En este artículo, vamos a explorar uno de los conceptos básicos de la matemática: la división.

Primero, es importante recordar que la multiplicación es sólo una suma repetida. Si tienes cinco veces dos, lo que estás haciendo es sumar dos cinco veces: dos más dos más dos más dos más dos. Esto nos da diez.

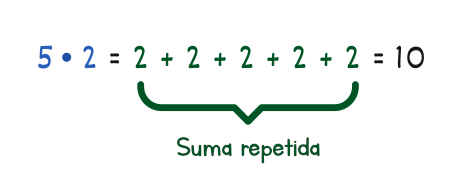
De la misma manera, la división es simplemente una resta repetida. Si tienes diez dividido por dos, sabes que la respuesta es cinco. Pero, ¿por qué? Porque cinco es el número de veces que puedes restar dos a diez hasta que llegas a cero, Observa este ejemplo.

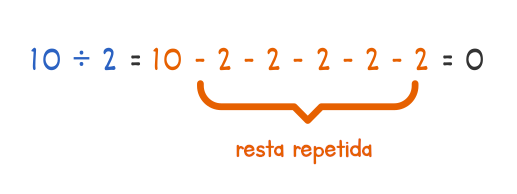
Si partimos de diez y le restamos dos en repetidas ocasiones, llegaremos finalmente a cero. Por ejemplo, si empezamos con 10 y le restamos 2, obtenemos 8. Si a continuación le restamos 2 nuevamente, obtenemos 6, y así sucesivamente. Finalmente, si restamos 2 menos 2, lo que equivale a una resta de cero, llegamos a cero.

Y la respuesta será la cantidad de veces que se ha restado el número dos.

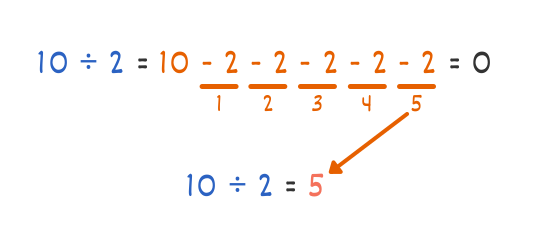
Veamos otro ejemplo. Si tienes 3 dividido por uno, eso significa que estás restando uno de 3 repetidamente hasta que llegas a cero. Si lo haces, descubrirás que tienes que restar tres veces para llegar a cero. Por lo tanto, 3 dividido por uno es igual a tres. ¿Interesante, no?

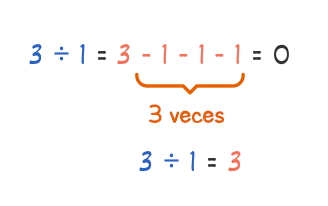
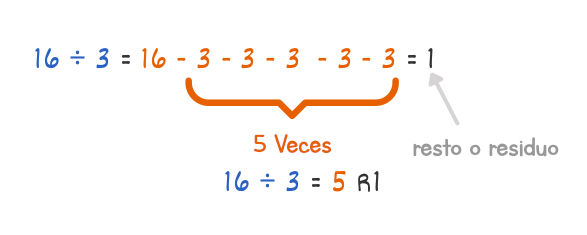
Pero, ¿qué sucede cuando no llegas a cero al hacer una resta repetida? Por ejemplo, considera 16 dividido entre tres. Si lo resuelves, tendrás que restar tres de 16 varias veces hasta que llegues a cero. Sin embargo, en este caso, no llegas a cero después de restar tres cinco veces. Llegas a uno. En este caso, el número que queda es el "resto o residuo". Los restos son la razón de ser de las fracciones, pero para ahora, puedes simplemente dejar el resto como uno y poner una R delante de él. Así que 16 dividido por tres sería igual a cinco R1.

Entonces, ¿por qué alguien inventó la división? Imagina que tienes 100 ositos de goma y quieres dividirlos en grupos de cinco. Si no tuvieras la división, tendrías que seguir restando manualmente cinco de 100 y contar el número de grupos. Eso llevaría una eternidad. Pero gracias a la división, puedes resolver rápidamente que 100 dividido por cinco es igual a 20 grupos de cinco.

¿Por qué no puedes dividir un número entre cero?

La vida está llena de infinitas posibilidades, pero hay una cosa que no podemos hacer: dividir nada entre cero, ni uno entre cero, ni ocho negativo entre cero, ni siquiera cero entre cero. ¿sabemos por qué?

Recuerda que la división no es más que una resta repetida, si quisieramos dividir diez dividido entre uno. Todo esto es diez menos uno, menos uno, hasta llegar a cero. ¿Cuántas veces restamos uno? Diez veces. Entonces, diez dividido por uno es diez.

Pero, ¿qué pasa si tenemos diez dividido por cero? Siguiendo la lógica anterior, todo esto es diez menos cero, menos cero, menos cero, hasta llegar a cero. ¿Cuántas veces restamos cero? Infinitas veces. Pero, como sabemos, no importa cuántas veces restemos cero de diez, nunca llegaremos a cero. Podemos restar cero cinco veces, 100 veces, infinitas veces, pero siempre nos mantendremos en diez. Por lo tanto, los matemáticos han declarado que la división por cero es indefinida.

Es común pensar que un número dividido por cero es cero o infinito, pero como hemos visto, es indefinido

En resumen, la división es simplemente una resta repetida. Si entiendes la idea de la resta repetida, entonces la división se vuelve mucho más fácil de entender. Y aunque la división puede no ser la operación matemática favorita de todos, estamos agradecidos de que alguien la haya inventado para hacernos la vida más fácil.

Si encuentras este contenido valioso, por favor ayúdame a llegar a más personas compartiéndolo en tus redes sociales.